수에 관한 덧셈, 뺄셈, 곱셈, 나눗셈 등 네 종류의 계산법을 사칙연산이라고 합니다. 수학의 기본이라고 할 수 있고, 이중 곱셈은 초등학교 저학년 과정에서 배우게 됩니다.
곱셈을 배우게 되면 실생활에서 바로 활용할 수 있습니다. 예를 들어서 진열장에 사과가 가로로 3줄, 세로로 4줄이 정렬되어 있을 때 하나하나 세어보지 않아도 곱셈을 이용해 3 X 4를 해주면 12개라는 답을 빠르게 구할 수 있습니다.

그런데 중학교에 들어가면 음수(0보다 작은 수)라는 개념을 배우게 됩니다. 음수는 0보다 작은 수로 숫자 앞에 부호 마이너스(-)를 붙여주어 사용합니다. 여기까지는 아무 문제가 없는데, 음수 곱하기 음수가 양수(0보다 큰 수)가 된다는 사실을 배우게 되면 상당히 혼란스러워집니다.
이 개념을 앞서 살펴본 실생활 응용에 똑같이 적용해보면 진열장에 사과가 가로로 -3줄, 세로로 -4줄이 정렬되어 있다는 것 자체가 이해하기 어렵고, 곱셈의 성질을 이용해 그 개수를 구하고자 했을 때 답이 앞서 구한 값과 같다는 사실은 이상하기까지 합니다. 그런데도 수학자들은 왜 음수 곱하기 음수를 양수라고 정의했을까요?

초등학교 때 위와 같은 곱셈의 성질을 배웁니다. 이 성질만을 이용해서 질문에 대한 답을 해결할 수 있는데, 먼저 (-1) 곱하기 0을 생각해보면 첫 번째 성질에 따라 0(ⓐ)이라는 값이 나와야 합니다.
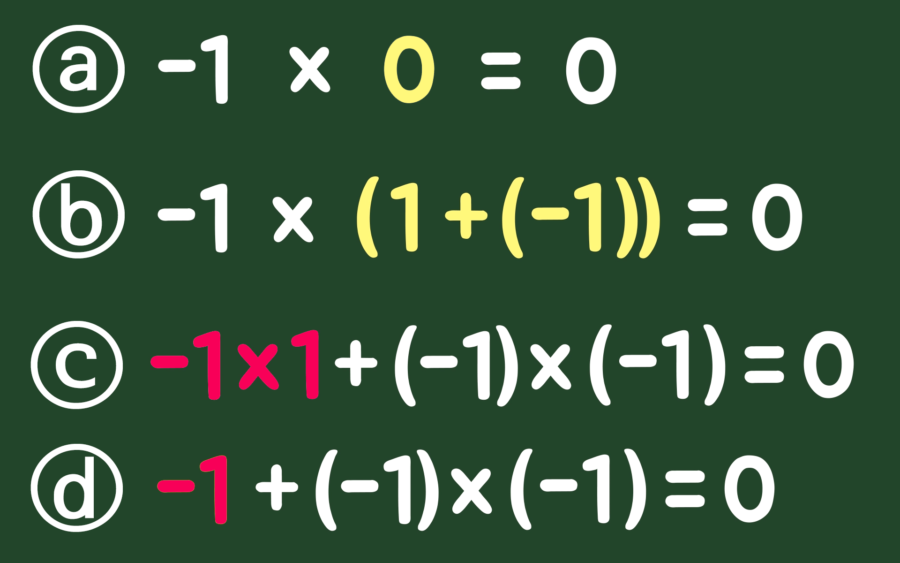
그런데 0은 1 더하기 -1로 표현할 수 있으므로 ⓑ와 같이 표현할 수도 있습니다. 여기서 분배법칙을 활용하면 ⓒ로도 표현할 수 있고, 이중 (-1)x(1)은 두 번째 성질에 따라서 자기 자신인 -1이 됩니다.
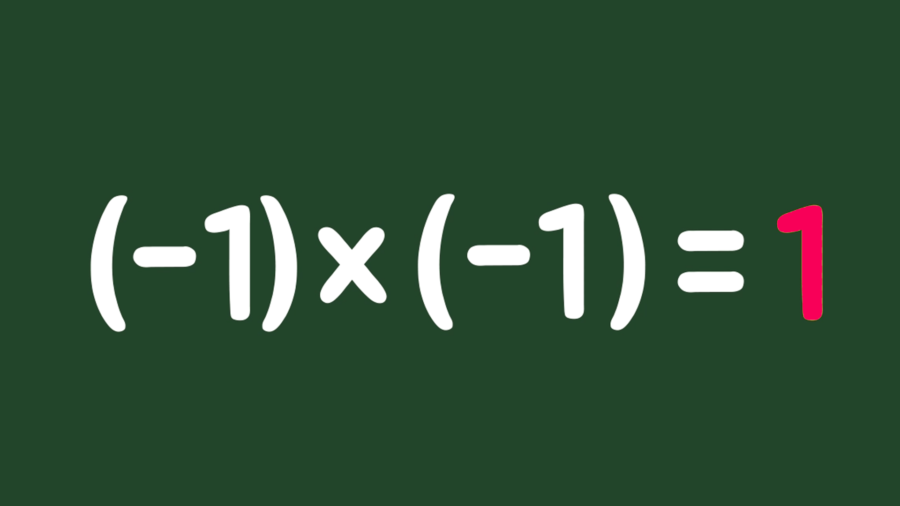
정리해보면 최종적으로 ⓓ식을 유도할 수 있고, 해당 식이 성립하려면 (-1)x(-1)이 1이어야 합니다. 즉, 곱셈의 성질을 보존하기 위해서는 음수와 음수의 곱을 양수로 정의하는 편이 자연스럽습니다.
이외에도 두 음수의 곱이 양수라는 사실을 증명하는 다양한 방법이 있으나 지금까지 알아본 논리가 가장 쉽고 간단해 널리 사용되는 증명입니다. 그런데 이와 같은 과정을 살펴봤다면 뭔가 찝찝할 겁니다. 개념을 마음대로 정의했고, 우리는 그것을 당연하게 받아들였으니 말입니다.

사실 곱셈은 0 이상의 특별한 수에만 적용되는 개념이었습니다. 하지만 곱셈의 성질을 유지하면서 논리를 전개해보면 0보다 작은 수에도 정의해줄 수 있고, 이처럼 기존의 개념에 관한 성질을 유지하면서 용법을 확장시키는 것을 수학에서는 ‘일반화’라고 합니다.
학창시절에 배웠지만 왜 그런지는 모르는 수학의 법칙들이 일반화의 산물이라고 할 수 있는데, 예를 들면 ‘0이 아닌 수의 0 제곱은 1이다.’, ‘1/2제곱은 루트다.’ 등이 해당합니다.
그러니까 일반화는 수학적 개념을 더 다양한 상황에서 쓸 수 있게 해주어 수학 이론을 더욱더 정교하게 만들어주는 중요한 기법입니다. 궁금증이 해결되셨나요?
Copyright. 사물궁이 잡학지식. All rights reserved

