팩토리얼(factorial)은 자연수(=양의 정수)의 계승이라고도 합니다. 기호는 느낌표(!)를 사용하고, n이 양의 정수일 때 1부터 n까지의 곱을 n!이라고 합니다.

예를 들어서 3!(=6)은 1×2×3이고, 4!(=24)은 1×2×3×4입니다. 이러한 정의에 따르면 0!은 0이어야 할 것 같은데, 0!은 1이라고 배우게 됩니다. 이유가 뭘까요?
팩토리얼의 성질을 이용하면 쉽게 증명할 수 있습니다. 앞서 언급한 3!에 4를 곱하면 4!이 됩니다. 수식으로 표현해보면 4×3!=4!이고, 양변에 4를 나눠주면 3!=4!÷4와 같이 정리할 수 있습니다.
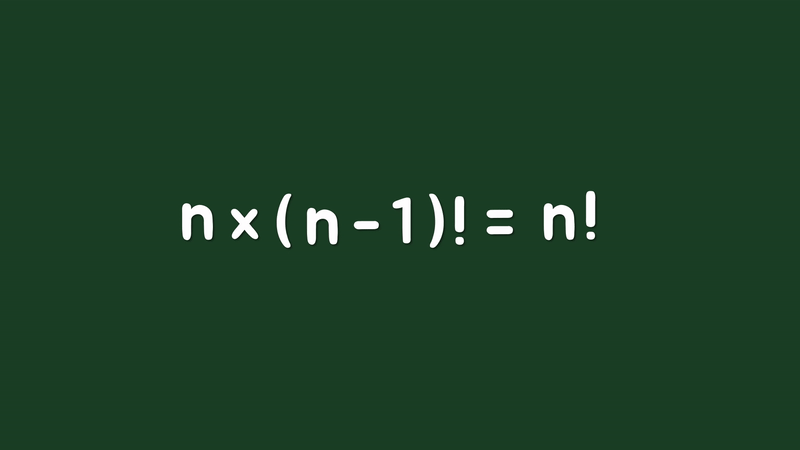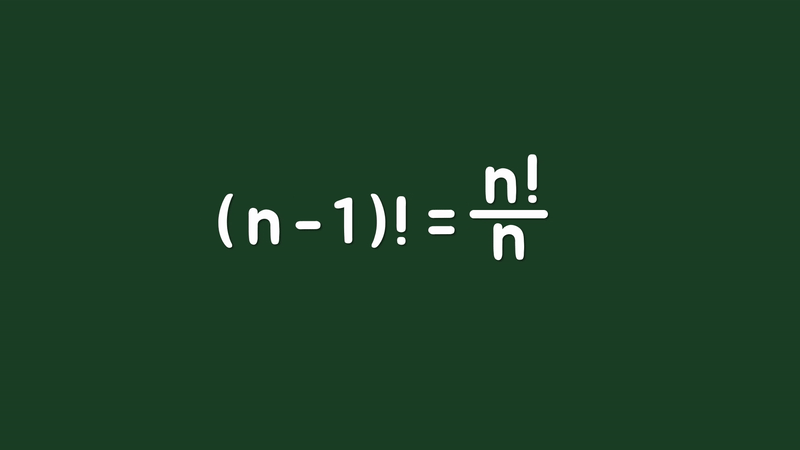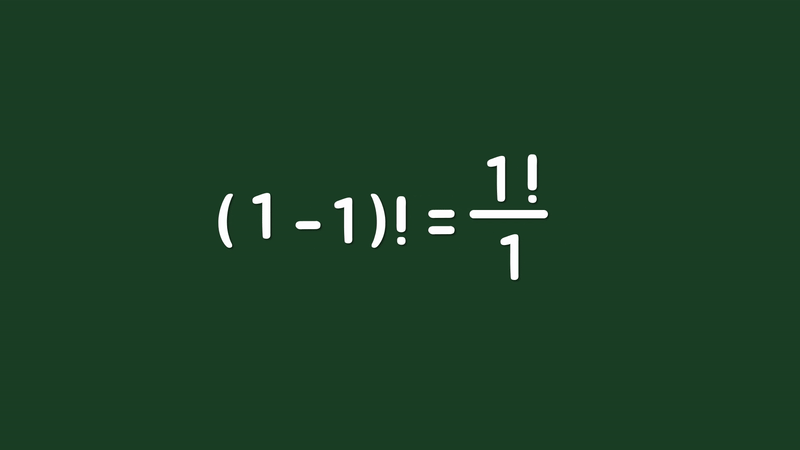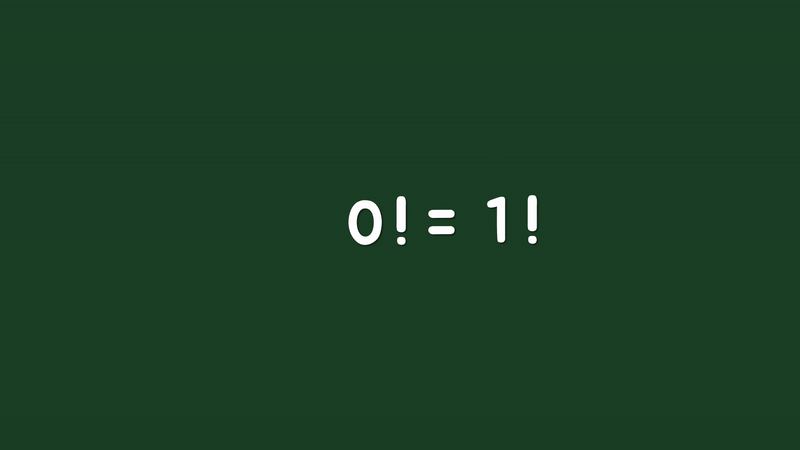
이 논리를 양의 정수 n으로 표현해보면 n×(n-1)!=n!와 같고, 똑같이 n으로 나눠주면 (n-1)!=n!÷n으로 정리할 수 있습니다. 그리고 n에 1을 대입해주면 0!은 1!÷1이 되고, 1!은 정의에 따라 1이므로 0!은 1이라는 값을 구할 수 있습니다.
이외에도 조합 공식을 이용해 증명하는 방법도 있습니다. ‘경우의 수’를 배울 때 나오는 개념으로 순서가 중요하지 않은 경우의 수를 구할 때 사용합니다. 예를 들면 n개의 대상 중 r개의 대상을 뽑을 때 nCr이라고 표기하고, 아래의 공식으로 원하는 값을 구할 수 있습니다.

공식만 보면 헷갈릴 수 있으니 4개의 대상 중 2개의 대상을 뽑는 상황에 적용해보면 ₄C₂ 라고 할 수 있고, 아래와 같이 풀 수 있습니다.

같은 방식으로 4개의 대상 중 4개의 대상을 뽑는다고 하면 ₄C₄가 되고, 당연히 한 가지 경우밖에 없기에 1이 나옵니다.

그런데 이 당연한 값을 수식으로 정리해보면 위와 같고, 분모와 분자를 4!로 나누면 1(=₄C₄)=1÷0!이 됩니다. 정리해보면 0!=1이라는 값을 구할 수 있습니다. 즉, 0!은 1입니다.
이렇게 정의한 이유는 이외에도 다양하겠으나 팩토리얼의 성질과 잘 부합하고, 팩토리얼이 사용된 공식들이 잘 작동하기 때문이라고 말할 수 있습니다.
그렇다면 팩토리얼은 0과 양의 정수에서만 정의할 수 있을까요? 그렇지는 않습니다. 18세기 스위스의 수학자 오일러는 팩토리얼을 모든 수에서 정의할 수 있도록 확장했고, 이렇게 만든 함수를 감마함수라고 했습니다.

이를 이용하면 모든 수에서 팩토리얼을 구할 수 있는데, 이런 값은 경우의 수를 구할 때 사용할 수는 없어도 미적분, 미분방정식, 복소해석학, 통계학, 정수론 등 다양한 수학 분야에서 널리 사용하고 있습니다. 궁금증이 해결되셨나요?
원고 투고 : 일리노이 대학교 시카고의 이론 수학 박사과정생 이성민
Copyright. 사물궁이 잡학지식. All rights reserved

