화장실에 가서 수도꼭지를 완전히 틀어주면 물줄기가 매우 강력하게 나오면서 울퉁불퉁해 보입니다. 이 상태를 난류 유동(Turbulent Flow)이라고 하고, 이 상태에서 수도꼭지를 점점 닫아보면 물줄기가 흐트러짐 없이 유리처럼 매끈하게 흐르는 것처럼 보이는데, 이 상태를 층류 유동(Laminar Flow)이라고 합니다.
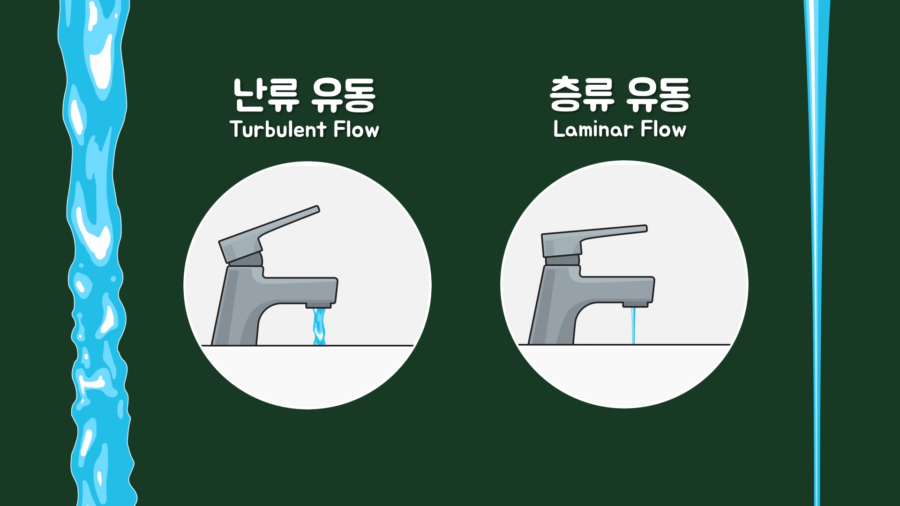
층류 유동 상태에서의 물줄기를 자세히 관찰해보면 물줄기가 아래로 갈수록 점점 가늘어진다는 사실을 알 수 있습니다. 이유가 뭘까요?

물줄기에 영향을 주는 요인에는 수압뿐만 아니라 중력도 있습니다. 물은 중력으로 인해 아래로 갈수록 점점 더 빨라지는데, 떨어지는 물 분자들간의 속도 차이가 점점 커지면서 물 분자들 사이의 거리도 점점 멀어질 수 있습니다.

그런데 물 분자들은 결합하려는 성질이 있어서 물 분자들끼리 결합을 유지한 채 빨라지는 물줄기를 따라 중심 쪽으로 점점 가늘어지게 됩니다.
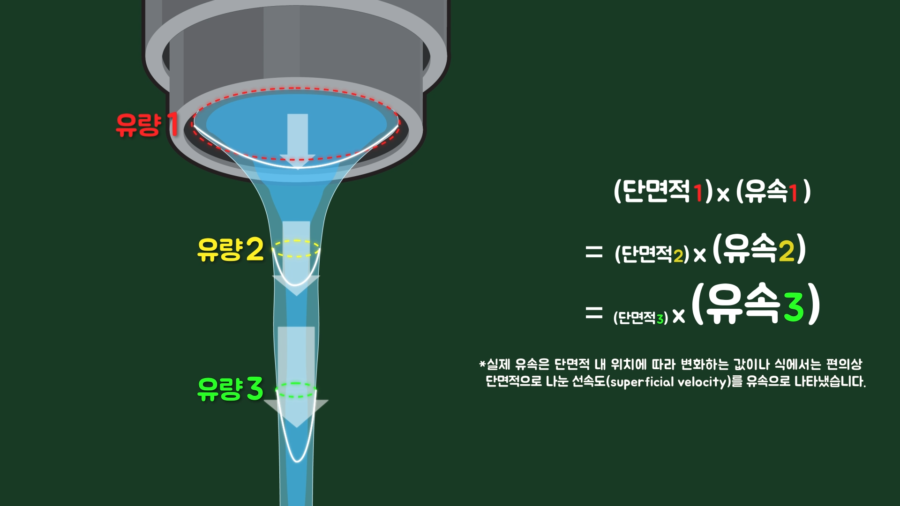
다음으로 해당 현상은 질량보존법칙 또는 연속방정식(continuity equation)으로도 해석할 수 있습니다. 만약 물줄기가 단위 시간 동안에 흐르는 양인 유량(Q= ρΔV /Δt)이 일정하다면 아래의 식을 만족합니다.
1, 2, 3의 지점이 있고, 지점에 해당하는 유량과 단면적, 유속이 보일 텐데, 중력에 의해 유속이 빨라지면 단면적과 유속의 곱은 일정하므로 단면적은 속도와 반대로 좁아지기에 물줄기가 가늘어진다는 결론이 나옵니다.
그렇다면 수도꼭지가 하늘 높은 곳에 있을 때는 떨어지는 물줄기가 계속 가늘어질 수 있을까요? 만약 그런 상황이 존재한다면 물줄기는 어느 순간 앞서가는 물을 더 이상 붙잡지 못해 끊어지고, 물방울이 됩니다.
이를 미립화(atomization)라고 하고, 분무기로 물을 분사할 때 물방울이 만들어지는 현상 등이 미립화의 예시입니다.

미립화 현상은 1833년 위 논문을 시작으로 활발하게 연구되어 왔습니다. 물줄기가 물방울로 분열되기까지의 거리를 나타낸 자료가 있는데, 아래 자료는 유속에 따라 분열길이를 나타내는 그래프 및 영역별 사진입니다.
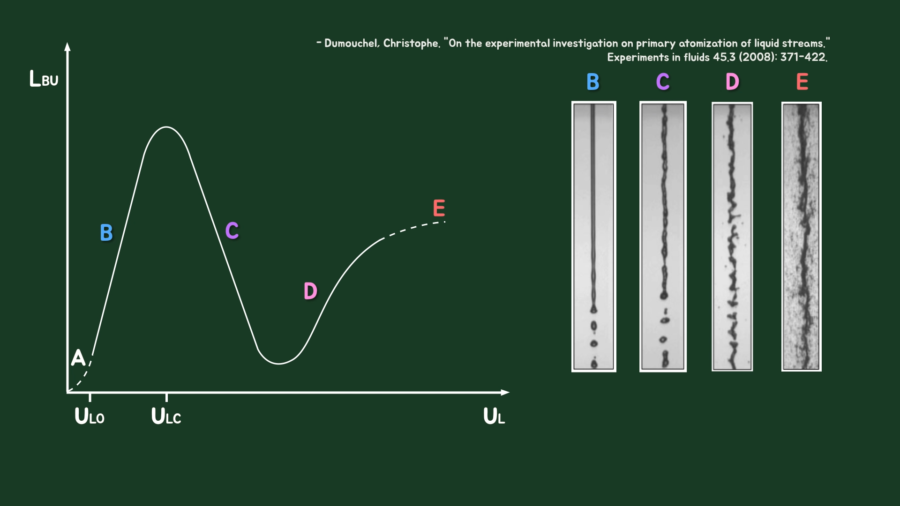
우리가 수도꼭지를 개방했을 때 보는 현상은 위 그래프 중 B 영역에 해당합니다. 이 구간의 물줄기는 낙하하다가 모세관 불안정성에 의해 출렁이기 시작하고, 출렁이는 표면 파동의 진폭이 물줄기의 반지름과 같아질 때 물방울로 떨어지는 영역입니다.
그리고 분열길이를 이론적으로 계산한 과학자들(Rayleigh, Weber)도 있는데, 아래와 같은 공식을 통해 구할 수 있습니다.

여기까지 주제의 의문을 해결해봤습니다. 미립화 현상은 공학적으로 매우 중요한 현상으로 다양한 분야에 응용됩니다.

대표적인 예시로 엔진의 경우 연료를 물방울(droplet) 형태로 분사해주면 부피 대비 넓은 면적으로 연료를 연소시켜 엔진 효율을 높여줄 수 있고, 잉크젯 프린터의 경우 한 방울씩 잉크를 떨어뜨려야 하므로 미립화 과정을 정확히 컨트롤해야 가능합니다.

일상에서 관찰할 수 있는 사소한 현상에서 시작해 다양한 분야에서 현상이 응용되는 것을 보니 참 놀랍습니다. 궁금증이 해결되셨나요?
– 원고 : 서울대학교 기계공학부 박사과정생 엔너드 EngNerd
Copyright. 사물궁이 잡학지식. All rights reserved



